Merkle Tree neden blok zincirde kullanılıyor?
Tüm programcılar veri yapılarının ve algoritmaların ne kadar önemli olduğu konusunda hemfikirdir.
Bu veri yapıları arasında en önemli olan ağaçlardır(trees). Bilgisayar bilimlerinde ağaçların kökü üst taraftadır.
Peki Merkle Tree nedir? Diğer ağaçlardan farklı olmasını sağlayan şey ne?
Tüm programcılar veri yapılarının ve algoritmaların ne kadar önemli olduğu konusunda hemfikirdir.
Bu veri yapıları arasında en önemli olan ağaçlardır(trees). Bilgisayar bilimlerinde ağaçların kökü üst taraftadır.
Peki Merkle Tree nedir? Diğer ağaçlardan farklı olmasını sağlayan şey ne?
Merkle Tree nedir?
Bu tür bir ağaçtan ilk kez 1980'lerin başlarında bahsedildi. Bu ağaç Ralph C Merkle tarafından yazılan Protocols for Public Key Cryptosystems yazısından sonra Merkle Tree olarak adlandırıldı. Ralph C Merkle yayınladığı yazıda, merkeziyetsiz bir ağda(P2P network) veri integrasyonunu onaylayabilmek için ağaç şeklinde bir veri yapısı kullanılabileceğine değindi.
Merkle Tree’den bahsetmeden önce hızlıca geleneksel ağaçlar ve hash fonksiyonları hakkında birkaç terime değinelim.
Merkle Tree’den bahsetmeden önce hızlıca geleneksel ağaçlar ve hash fonksiyonları hakkında birkaç terime değinelim.
1 — Ağaç veri yapıları hakkında kısa bir giriş
Bazı veri hiyerarşilerini göstermemiz gerektiğinde ağaçları kullanırız. Ağaçlar dosya yapılarının saklanmasında, XML/HTML verilerinde vb. yaygın olarak kullanılırlar.
Aşağıdaki görselde bir ağaç örneği verilmiştir.
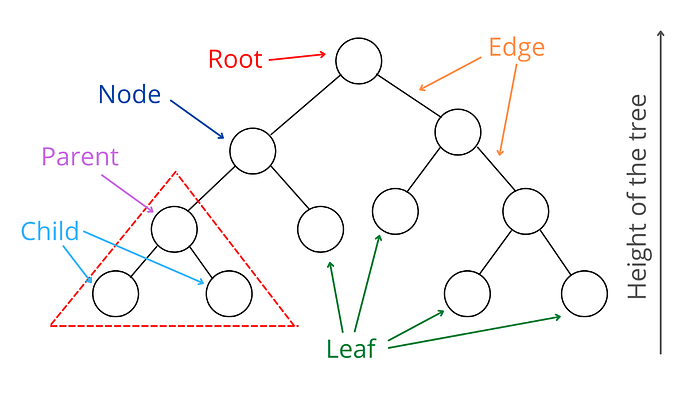
Ağaçla ilgili olan bazı terimler:
Nodes: Bir ağaçtaki her bir birey node(düğüm) olarak adlandırılır.
Edge: Düğümler(nodes) arasındaki çizgiler edge olarak adlandırılır.
Root: Bir ağacın tepesindeki düğüm root olarak adlandırılır. Her operasyon root düğümünden başlar.
Parents and Child nodes: Ebeveyn düğümler(parent nodes) atlarında kendilerine bağlı bir veya daha fazla düğüm bulunduran düğümlerdir. Ebeveyn düğümlerin altındaki düğümler ise çocuk düğümler(child nodes) olarak adlandırılır.
Leaf nodes: Ağacın altındaki düğümlere leaf nodes denir.
Aşağıdaki görselde bir ağaç örneği verilmiştir.

Ağaçla ilgili olan bazı terimler:
Nodes: Bir ağaçtaki her bir birey node(düğüm) olarak adlandırılır.
Edge: Düğümler(nodes) arasındaki çizgiler edge olarak adlandırılır.
Root: Bir ağacın tepesindeki düğüm root olarak adlandırılır. Her operasyon root düğümünden başlar.
Parents and Child nodes: Ebeveyn düğümler(parent nodes) atlarında kendilerine bağlı bir veya daha fazla düğüm bulunduran düğümlerdir. Ebeveyn düğümlerin altındaki düğümler ise çocuk düğümler(child nodes) olarak adlandırılır.
Leaf nodes: Ağacın altındaki düğümlere leaf nodes denir.
2 — Hash Fonkisyonları
Hashing giriş verisinin düzeltilmiş boyuttaki çıkış verisine dönüştürme işlemine verilen addır. (Hash value)
Hash değerleri numaralar ve harfleri içerir fakat özel karakterleri içermez.
Hash’leri kullanmanın yararlı tarafı temsil edilen verinin daha az hafıza tüketerek saklanmasıdır.
Hash fonksiyonlarının bazı önemli özellikleri:
Hash değerleri numaralar ve harfleri içerir fakat özel karakterleri içermez.
Hash’leri kullanmanın yararlı tarafı temsil edilen verinin daha az hafıza tüketerek saklanmasıdır.
Hash fonksiyonlarının bazı önemli özellikleri:
- Geri döndürülemezler, yani gerçek verileri hash değerinden bulamayız.
- Verideki küçük bir değişim hash değerinde tamamen farklı bir değerin oluşmasıyla sonuçlanacaktır.(En küçük değişimde bile hash değeri değişir)
- Özdeş veriler her zaman aynı hash değerini üretir.Verileri tersine çeviremeyeceğiniz için bu, veri bütünlüğünü kontrol etmek için çok önemlidir.

Merkle Tree
Bir Merkle tree’de her düğüm(node) altındaki çocuk düğümlerin(child nodes) hash değerlerini temsil eder. Tüm ağaç ,leaf düğümlerinin hash değerleriyle, aşağıdan yukarıya doğru ,root düğümüne ulaşana kadar, devam eder.
Bir Merkle Tree inşa etmek için gerekli algoritma:
1- Listedeki tüm verilerin hash değerlerini hesapla.
2- Sol taraftan başlayarak sağa doğru iki hash değerini bir grup haline getir.(2 hash değeri bir grup oluşturur.)
3- Bir gruptaki hash değerlerini birleştirin ve hash değerini hesapla.
4- 2. ve 3. adımları sadece 1 düğüm kalana kadar(root node kalana kadar) tekrarla.
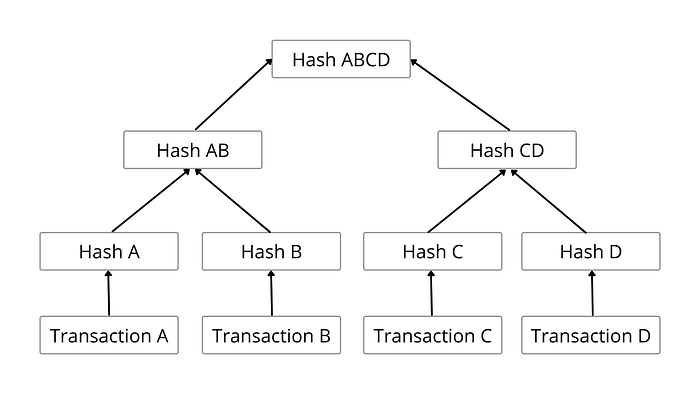

Bir Merkle Tree inşa etmek için gerekli algoritma:
1- Listedeki tüm verilerin hash değerlerini hesapla.
2- Sol taraftan başlayarak sağa doğru iki hash değerini bir grup haline getir.(2 hash değeri bir grup oluşturur.)
3- Bir gruptaki hash değerlerini birleştirin ve hash değerini hesapla.
4- 2. ve 3. adımları sadece 1 düğüm kalana kadar(root node kalana kadar) tekrarla.


Merkle Tree’de arama yapmak
Merkle Tree’de bulunan bir işlemin veya verinin var olup olmadığını ağaçtaki tüm verileri incelemeden kolaylıkla kontrol edebilirsiniz. Bu yöntem Katılım Kanıtı(Proof of Inclusion) olarak adlandırılır.
Diyelim ki A’dan H’ye bazı işlemlerin bir Merkle ağacı var. Ve bizim de Merkle köküne(root) erişimimiz var. Şimdi ağaçta G olup olmadığını araştırmamız gerekiyor. G işleminin hashini kolayca hesaplayabiliriz. Artık kök düğüme giden yolu izleyerek hash(G)’den kök hash’i yeniden hesaplayabiliriz.

Diyelim ki A’dan H’ye bazı işlemlerin bir Merkle ağacı var. Ve bizim de Merkle köküne(root) erişimimiz var. Şimdi ağaçta G olup olmadığını araştırmamız gerekiyor. G işleminin hashini kolayca hesaplayabiliriz. Artık kök düğüme giden yolu izleyerek hash(G)’den kök hash’i yeniden hesaplayabiliriz.

Kök düğüme(Root node) giden yol nasıl izlenir?
Her bir düğüm için, üst düğüme giden başka bir çift olduğunu biliyoruz.
G’nin durumunda bu H’dır. Eğer H’ın hash değerini elde edebilirsek GH’ın hash’ini hesaplayabiliriz. Sonrasında ana düğüme ulaşmak için GH’nin hashine ve EF’nin hashine ihtiyaç vardır.(EFGH). Sonunda kök hash’i hesaplayabilmek için ABCD’nin hashine ihtiyaç vardır.(ABCDEFGH)
Elde edilen kök hashi verilen merkle tree kök hashine eşitse G işleminin Merkle Tree’ye dahil edildiği anlamına gelir.
Tüm işlem için, tüm ağdaki işlemlerin kopyasını indirmeden sorgulayabileceğimiz 3 hashe ihtiyacımız vardır. Bu hafıza ve zaman kazandırır. Merkle Tree’de arama yapmanın en karmaşık kısmı O(log N)dir.

Merkle Tree’nin Blok zincir ile bağlantısı nasıldır?
Blok zincir P2P bir ağ üzerine kurulmuş olan, dağıtılmış bir kayıt depolama tekniğidir. Bir sürü bilgi içeren blok bir liste gibidir. Her bir blok header(başlık) ve body(gövde) kısımlarına sahiptir. Başlık bloktaki bilgileri saklar, gövde ise gerçek verileri veya işlemleri içerir.
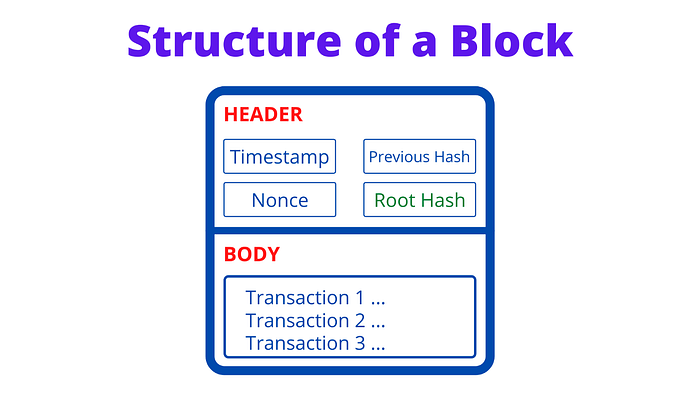
Bir blok başlığı(header) bloğun hash değerini, önceki bloğun hash değerini, zaman dalgasını, nonce’unu, zorluk bitini, yazılımın versiyonunu ve kök hashi içerir.
Kök hash blokta depolanmış verinin veya işlemlerin temsil edildiği eşsiz bir şeydir. Ve Merkle Tree kullanılarak hesaplanır. Blokta depolanmış tüm işlemler kullanılarak bir Merkle Tree oluşturulur ve Merkle kökü(Merkle root) kök hashinde(root hash)depolanır.

G’nin durumunda bu H’dır. Eğer H’ın hash değerini elde edebilirsek GH’ın hash’ini hesaplayabiliriz. Sonrasında ana düğüme ulaşmak için GH’nin hashine ve EF’nin hashine ihtiyaç vardır.(EFGH). Sonunda kök hash’i hesaplayabilmek için ABCD’nin hashine ihtiyaç vardır.(ABCDEFGH)
Elde edilen kök hashi verilen merkle tree kök hashine eşitse G işleminin Merkle Tree’ye dahil edildiği anlamına gelir.
Tüm işlem için, tüm ağdaki işlemlerin kopyasını indirmeden sorgulayabileceğimiz 3 hashe ihtiyacımız vardır. Bu hafıza ve zaman kazandırır. Merkle Tree’de arama yapmanın en karmaşık kısmı O(log N)dir.

Merkle Tree’nin Blok zincir ile bağlantısı nasıldır?
Blok zincir P2P bir ağ üzerine kurulmuş olan, dağıtılmış bir kayıt depolama tekniğidir. Bir sürü bilgi içeren blok bir liste gibidir. Her bir blok header(başlık) ve body(gövde) kısımlarına sahiptir. Başlık bloktaki bilgileri saklar, gövde ise gerçek verileri veya işlemleri içerir.

Bir blok başlığı(header) bloğun hash değerini, önceki bloğun hash değerini, zaman dalgasını, nonce’unu, zorluk bitini, yazılımın versiyonunu ve kök hashi içerir.
Kök hash blokta depolanmış verinin veya işlemlerin temsil edildiği eşsiz bir şeydir. Ve Merkle Tree kullanılarak hesaplanır. Blokta depolanmış tüm işlemler kullanılarak bir Merkle Tree oluşturulur ve Merkle kökü(Merkle root) kök hashinde(root hash)depolanır.

Kök hash’inin işlem doğrulanmasındaki rolü
Blok zincirinin doğası her bir katılımcının zincirin lokal kopyasını tutmasını gerektirir. Bu sebeple, bir bloktaki tüm işlemleri doğrulayacak bir mekanizmaya ihtiyaç vardır. Burada Merkle Tree oyuna dahil olur.
Bir blok zincirde, iki kullanıcı arasında ne zaman bir işlem gerçekleşirse, bu ağdaki tüm düğümlere yayımlanır. Bu sayede tüm düğümler işlemleri doğrulayabilirler ve işlemleri kendi lokallerine kopya olarak ekleyebilirler.
Eğer birisi işlemi doğrulamak isterse tek yapması gereken işlemin hashini Merkle Tree’de aratmaktır. Bu arama ve doğrulama operasyonu Simplified Payment Verification(SPV) olarak adlandırılan özel bir düğüm sayesinde gerçekleştirilir. SPV düğümleri ağdan sadece blok başlıklarını indirirler. Merkle yolunu kullanarak bir işlemin ağda olup olmadığını doğrulayabilirler.
Bir blok zincirde, iki kullanıcı arasında ne zaman bir işlem gerçekleşirse, bu ağdaki tüm düğümlere yayımlanır. Bu sayede tüm düğümler işlemleri doğrulayabilirler ve işlemleri kendi lokallerine kopya olarak ekleyebilirler.
Eğer birisi işlemi doğrulamak isterse tek yapması gereken işlemin hashini Merkle Tree’de aratmaktır. Bu arama ve doğrulama operasyonu Simplified Payment Verification(SPV) olarak adlandırılan özel bir düğüm sayesinde gerçekleştirilir. SPV düğümleri ağdan sadece blok başlıklarını indirirler. Merkle yolunu kullanarak bir işlemin ağda olup olmadığını doğrulayabilirler.
Simplified Payment Verification(SPV) = Basitleştirilmiş Ödeme Doğrulaması

Kök hash blok zincir için neden bu kadar önemli?
Kök hashler önemlidir çünkü blok zincir için yararlı olan belirli özelliklere sahiptirler. Bu özelliklerin ne olduğuna bir bakalım:
- Arama işlemleri gerçek veriler yerine hash değerleri üzerinden gerçekleştirilir. Hash değerleri, gerçek verilerdeki küçük bir değişiklik için bile tamamen değişir. Hash değerinin bu özelliği, herhangi bir değişikliği çok kolay bir şekilde tanımlamaya yardımcı olur.
- Arama işlemi çok etkilidir. 500 işlemlik bir liste için, bir blokta bir işlemin olup olmadığını doğrulamak için en fazla 9 hash değerine ihtiyacımız olur. Arama işleminin en kötü durum karmaşıklığı O(log N)’dir. Aksi takdirde, O(N) karmaşıklığı alacak işlemi lineer olarak bulmamız gerekir.
- SPV düğümleri Merkle Tree’ye güvenir ve doğrulamayı yalnızca blok başlıklarını indirerek yapar. Aksi takdirde, bu düğümlerin doğrulama amacıyla blok zincirinin tüm kopyasını indirmesi gerekir. Bu, yüksek ağ trafiğine yol açacak ve çok daha fazla depolama kapasitesi gerektirecektir.
- Hash değerleri ayrıca Merkle Tree’nin depolanmasına ve zaman verimliliğine de katkıda bulunur. Bir işlemdeki herhangi bir değişiklik, kök hash’i değiştirecek ve sonuç olarak bloğun hash’ini değiştirecektir ve kendinden sonra gelen tüm zincirleri değiştirecektir.









